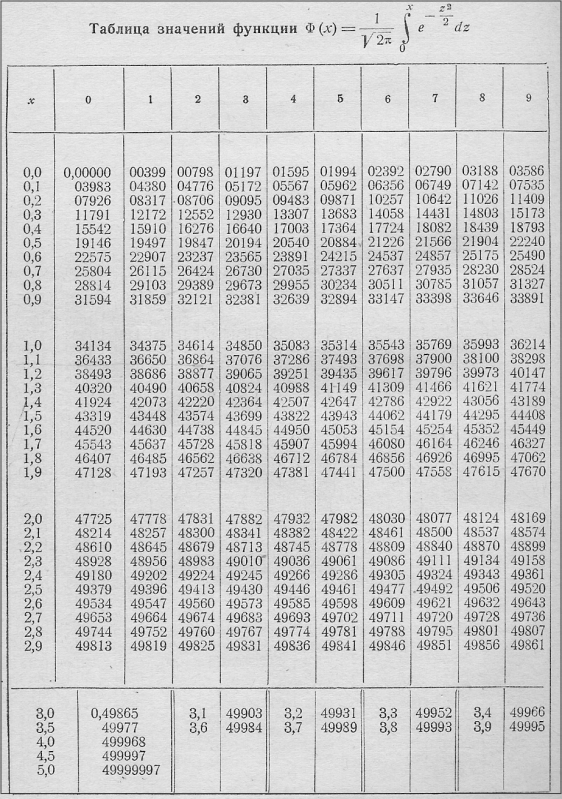
1. Плотность распределения среднедушевого дохода x в логарифмическом масштабе (a - средне-логарифмическое значение среднедушевого дохода, б_ln - логарифмическая дисперсия, определяется с помощью таблицы интеграла вероятности Ф(z) (см. ниже), где z = (ln x - ln a)/б_ln, и уравнения n - 0,5 = Ф(z), где n - доля населения, среднедушевой доход которого не выше х):

dw/d(ln x) = dn/d(ln x)=((2п)^1/2б_ln)^-1e^{-(ln x - ln a)2/(2б_ln 2)}

2. Плотость распределения энтропии власти:

ds/d(ln x) = d(ln w)/d(ln x ) = - (2(2п)^1/2б_ln³)^-1(ln x - ln a)²

3. Удельная энтропия власти в интервале около центра распределения (ln a - E, ln a + E), Е=1:

s_c = - (3(2п)^1/2)^-1(Е/б_ln)³ (результат интегрирования).

4. Аппроксимация разности интегралов вероятности для его значений аргумента z более 4,0:

u = Ф(z_о) - Ф(z) = k₄ (z_о - z) ⁴ + k₆ (z_о - z)⁶,

где k₄ = 1,3990*10^-6, k₆ = 4,4994*10^-6, z_о = 5,3522.

5. Оценка степени антагонизма в Стране: отношение условно самого высокого среднедушевого дохода x_max к условно самому низкому его значению x_min, не менее:

A = x_max/ x_min = e ^2б_lnz_m,

где б_ln - логарифмическая дисперсия, а z_m равно:

z_m = z_о - Dz,

Величина Dz вычисляется методом последовательных приближений:

Dz_i+1 = (u_о/(k₄ + k₆Dz_i²))^1/4,

Величина же u_о вычисляется по формуле u_о = 1/N, где N - численность населения.

Таблица со значениями интеграла вероятности (взята из книги Б.В.Гнеденко "Курс теории вероятностей")